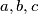
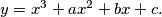
Real constants are such that there is exactly one square all of whose vertices lie on the cubic curve Prove that the square has sides of length
%V0
Real constants $a, b, c$ are such that there is exactly one square all of whose vertices lie on the cubic curve $y = x^3 + ax^2 + bx + c.$ Prove that the square has sides of length $\sqrt[4]{72}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
are such that there is exactly one square all of whose vertices lie on the cubic curve 
Prove that the square has sides of length ![\sqrt[4]{72}.](/media/m/5/4/c/54c66832c053970e63876cd79459f032.png)