IMO Shortlist 1991 problem 22
Dodao/la:
arhiva2. travnja 2012. Let

and

be two integer-valued functions defined on the set of all integers such that
(a)
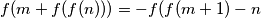
for all integers

and
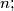
(b)

is a polynomial function with integer coefficients and g(n) =
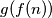
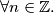
%V0
Let $f$ and $g$ be two integer-valued functions defined on the set of all integers such that
(a) $f(m + f(f(n))) = -f(f(m+ 1) - n$ for all integers $m$ and $n;$
(b) $g$ is a polynomial function with integer coefficients and g(n) = $g(f(n))$ $\forall n \in \mathbb{Z}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991