IMO Shortlist 1991 problem 24
Dodao/la:
arhiva2. travnja 2012. Suppose that

and
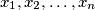
are real numbers between 0 and 1 (inclusive). Prove that for some index

between

and
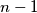
the
inequality
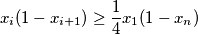
%V0
Suppose that $n \geq 2$ and $x_1, x_2, \ldots, x_n$ are real numbers between 0 and 1 (inclusive). Prove that for some index $i$ between $1$ and $n - 1$ the
inequality
$$x_i (1 - x_{i+1}) \geq \frac{1}{4} x_1 (1 - x_{n})$$
Izvor: Međunarodna matematička olimpijada, shortlist 1991