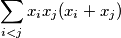
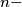
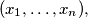
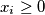
Determine the maximum value of the sum over all tuples satisfying and
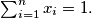
%V0
Determine the maximum value of the sum
$$\sum_{i < j} x_ix_j (x_i + x_j)$$
over all $n -$tuples $(x_1, \ldots, x_n),$ satisfying $x_i \geq 0$ and $\sum^n_{i = 1} x_i = 1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
tuples 
satisfying 
and 