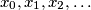
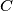
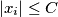
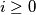
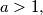
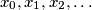
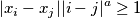
An infinite sequence of real numbers is said to be bounded if there is a constant such that for every . Given any real number construct a bounded infinite sequence such that for every pair of distinct nonnegative integers .
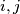
%V0
An infinite sequence $\,x_{0},x_{1},x_{2},\ldots \,$ of real numbers is said to be bounded if there is a constant $\,C\,$ such that $\, \vert x_{i} \vert \leq C\,$ for every $\,i\geq 0$. Given any real number $\,a > 1,\,$ construct a bounded infinite sequence $x_{0},x_{1},x_{2},\ldots \,$ such that
$$\vert x_{i} - x_{j} \vert \vert i - j \vert^{a}\geq 1$$
for every pair of distinct nonnegative integers $i, j$.
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
of real numbers is said to be bounded if there is a constant 
such that 
for every 
. Given any real number 
construct a bounded infinite sequence 
such that 
.