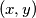
Prove that for any positive integer there exist an infinite number of pairs of integers such that
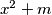
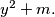
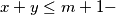
(i) and are relatively prime; (ii) divides ; (iii) divides (iv) (optional condition)
%V0
Prove that for any positive integer $m$ there exist an infinite number of pairs of integers $(x, y)$ such that
(i) $x$ and $y$ are relatively prime;
(ii) $y$ divides $x^2 + m$;
(iii) $x$ divides $y^2 + m.$
(iv) $x + y \leq m + 1-$ (optional condition)
Izvor: Međunarodna matematička olimpijada, shortlist 1992
Školjka 
there exist an infinite number of pairs of integers 
such that 
and 
are relatively prime; 
; 
(optional condition)