IMO Shortlist 1992 problem 2
Dodao/la:
arhiva2. travnja 2012. Let
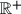
be the set of all non-negative real numbers. Given two positive real numbers

and
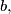
suppose that a mapping
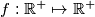
satisfies the functional equation:
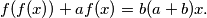
Prove that there exists a unique solution of this equation.
%V0
Let $\mathbb{R}^+$ be the set of all non-negative real numbers. Given two positive real numbers $a$ and $b,$ suppose that a mapping $f: \mathbb{R}^+ \mapsto \mathbb{R}^+$ satisfies the functional equation:
$$f(f(x)) + af(x) = b(a + b)x.$$
Prove that there exists a unique solution of this equation.
Izvor: Međunarodna matematička olimpijada, shortlist 1992