IMO Shortlist 1992 problem 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 The diagonals of a quadrilateral  are perpendicular:
are perpendicular: 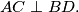 Four squares,
Four squares, 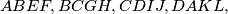 are erected externally on its sides. The intersection points of the pairs of straight lines
are erected externally on its sides. The intersection points of the pairs of straight lines 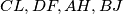 are denoted by
are denoted by 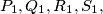 respectively (left figure), and the intersection points of the pairs of straight lines
respectively (left figure), and the intersection points of the pairs of straight lines 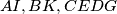 are denoted by
are denoted by 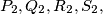 respectively (right figure). Prove that
respectively (right figure). Prove that 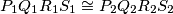 where
where 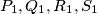 and
and 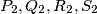 are the two quadrilaterals.
are the two quadrilaterals.
Alternative formulation: Outside a convex quadrilateral with perpendicular diagonals, four squares
with perpendicular diagonals, four squares 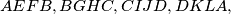 are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals
are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals 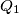 and
and 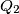 formed by the lines
formed by the lines 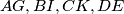 and
and 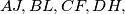 respectively, are congruent.
respectively, are congruent.
 are perpendicular:
are perpendicular: 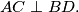 Four squares,
Four squares, 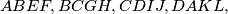 are erected externally on its sides. The intersection points of the pairs of straight lines
are erected externally on its sides. The intersection points of the pairs of straight lines 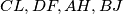 are denoted by
are denoted by 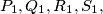 respectively (left figure), and the intersection points of the pairs of straight lines
respectively (left figure), and the intersection points of the pairs of straight lines 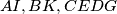 are denoted by
are denoted by 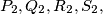 respectively (right figure). Prove that
respectively (right figure). Prove that 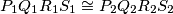 where
where 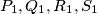 and
and 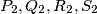 are the two quadrilaterals.
are the two quadrilaterals. Alternative formulation: Outside a convex quadrilateral
 with perpendicular diagonals, four squares
with perpendicular diagonals, four squares 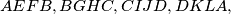 are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals
are constructed (vertices are given in counterclockwise order). Prove that the quadrilaterals 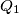 and
and 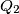 formed by the lines
formed by the lines 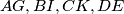 and
and 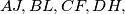 respectively, are congruent.
respectively, are congruent. Izvor: Međunarodna matematička olimpijada, shortlist 1992
 Školjka
Školjka 
