IMO Shortlist 1992 problem 7
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Two circles 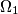 and
and 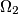 are externally tangent to each other at a point
are externally tangent to each other at a point  , and both of these circles are tangent to a third circle
, and both of these circles are tangent to a third circle 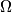 which encloses the two circles
which encloses the two circles 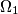 and
and 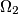 .
.
The common tangent to the two circles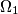 and
and 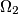 at the point
at the point  meets the circle
meets the circle 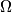 at a point
at a point  . One common tangent to the circles
. One common tangent to the circles 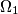 and
and 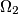 which doesn't pass through
which doesn't pass through  meets the circle
meets the circle 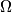 at the points
at the points  and
and  such that the points
such that the points  and
and  lie on the same side of the line
lie on the same side of the line  .
.
Prove that the point is the incenter of triangle
is the incenter of triangle  .
.
Alternative formulation. Two circles touch externally at a point . The two circles lie inside a large circle and both touch it. The chord
. The two circles lie inside a large circle and both touch it. The chord  of the large circle touches both smaller circles (not at
of the large circle touches both smaller circles (not at  ). The common tangent to the two smaller circles at the point
). The common tangent to the two smaller circles at the point  meets the large circle at a point
meets the large circle at a point  , where the points
, where the points  and
and  are on the same side of the chord
are on the same side of the chord  . Show that the point
. Show that the point  is the incenter of triangle
is the incenter of triangle  .
.
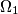 and
and 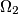 are externally tangent to each other at a point
are externally tangent to each other at a point  , and both of these circles are tangent to a third circle
, and both of these circles are tangent to a third circle 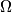 which encloses the two circles
which encloses the two circles 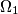 and
and 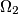 .
. The common tangent to the two circles
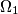 and
and 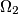 at the point
at the point  meets the circle
meets the circle 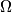 at a point
at a point  . One common tangent to the circles
. One common tangent to the circles 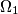 and
and 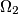 which doesn't pass through
which doesn't pass through  meets the circle
meets the circle 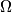 at the points
at the points  and
and  such that the points
such that the points  and
and  lie on the same side of the line
lie on the same side of the line  .
. Prove that the point
 is the incenter of triangle
is the incenter of triangle  .
. Alternative formulation. Two circles touch externally at a point
 . The two circles lie inside a large circle and both touch it. The chord
. The two circles lie inside a large circle and both touch it. The chord  of the large circle touches both smaller circles (not at
of the large circle touches both smaller circles (not at  ). The common tangent to the two smaller circles at the point
). The common tangent to the two smaller circles at the point  meets the large circle at a point
meets the large circle at a point  , where the points
, where the points  and
and  are on the same side of the chord
are on the same side of the chord  . Show that the point
. Show that the point  is the incenter of triangle
is the incenter of triangle  .
. Izvor: Međunarodna matematička olimpijada, shortlist 1992
 Školjka
Školjka 
