IMO Shortlist 1992 problem 8
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Show that in the plane there exists a convex polygon of 1992 sides satisfying the following conditions:
(i) its side lengths are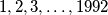 in some order;
in some order;
(ii) the polygon is circumscribable about a circle.
Alternative formulation: Does there exist a 1992-gon with side lengths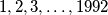 circumscribed about a circle? Answer the same question for a 1990-gon.
circumscribed about a circle? Answer the same question for a 1990-gon.
(i) its side lengths are
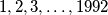 in some order;
in some order; (ii) the polygon is circumscribable about a circle.
Alternative formulation: Does there exist a 1992-gon with side lengths
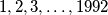 circumscribed about a circle? Answer the same question for a 1990-gon.
circumscribed about a circle? Answer the same question for a 1990-gon. Izvor: Međunarodna matematička olimpijada, shortlist 1992
 Školjka
Školjka 
