IMO Shortlist 1992 problem 12
Dodao/la:
arhiva2. travnja 2012. Let
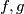
and

be polynomials with real coefficients,

and
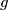
in one variable and

in two variables. Suppose
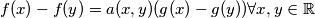
Prove that there exists a polynomial

with
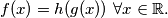
%V0
Let $f, g$ and $a$ be polynomials with real coefficients, $f$ and $g$ in one variable and $a$ in two variables. Suppose
$$f(x) - f(y) = a(x, y)(g(x) - g(y)) \forall x,y \in \mathbb{R}$$
Prove that there exists a polynomial $h$ with $f(x) = h(g(x)) \text{ } \forall x \in \mathbb{R}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1992