IMO Shortlist 1992 problem 14
Dodao/la:
arhiva2. travnja 2012. For any positive integer

define
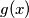
as greatest odd divisor of
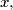
and
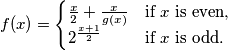
Construct the sequence
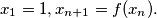
Show that the number 1992 appears in this sequence, determine the least

such that
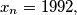
and determine whether

is unique.
%V0
For any positive integer $x$ define $g(x)$ as greatest odd divisor of $x,$ and $$f(x) =\begin{cases}\frac{x}{2}+\frac{x}{g(x)}&\text{if\ \(x\) is even},\\ 2^{\frac{x+1}{2}}&\text{if\ \(x\) is odd}.\end{cases}$$
Construct the sequence $x_1 = 1, x_{n + 1} = f(x_n).$ Show that the number 1992 appears in this sequence, determine the least $n$ such that $x_n = 1992,$ and determine whether $n$ is unique.
Izvor: Međunarodna matematička olimpijada, shortlist 1992