IMO Shortlist 1992 problem 18
Dodao/la:
arhiva2. travnja 2012. Let
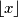
denote the greatest integer less than or equal to

Pick any

in
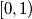
and define the sequence
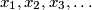
by
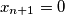
if
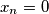
and
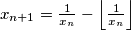
otherwise. Prove that
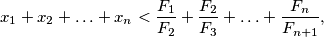
where
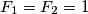
and
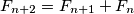
for
%V0
Let $\lfloor x \rfloor$ denote the greatest integer less than or equal to $x.$ Pick any $x_1$ in $[0, 1)$ and define the sequence $x_1, x_2, x_3, \ldots$ by $x_{n+1} = 0$ if $x_n = 0$ and $x_{n+1} = \frac{1}{x_n} - \left \lfloor \frac{1}{x_n} \right \rfloor$ otherwise. Prove that
$$x_1 + x_2 + \ldots + x_n < \frac{F_1}{F_2} + \frac{F_2}{F_3} + \ldots + \frac{F_n}{F_{n+1}},$$
where $F_1 = F_2 = 1$ and $F_{n+2} = F_{n+1} + F_n$ for $n \geq 1.$
Izvor: Međunarodna matematička olimpijada, shortlist 1992