IMO Shortlist 1993 problem A1
Dodao/la:
arhiva2. travnja 2012. Define a sequence
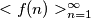
of positive integers by
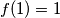
and
{{ INVALID LATEX }}
for
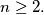
Let
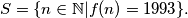
(i) Prove that

is an infinite set.
(ii) Find the least positive integer in
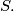
(iii) If all the elements of

are written in ascending order as
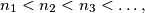
show that
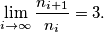
%V0
Define a sequence $<f(n)>^{\infty}_{n=1}$ of positive integers by $$f(1) = 1$$ and
$f(n) =\left\{\begin{array}{ll}f(n-1)-n &\text{ if }f(n-1) > n;\\ f(n-1)+n &\text{ if }f(n-1)\leq n,\end{array}\right$
for $n \geq 2.$ Let $S = \{n \in \mathbb{N} | f(n) = 1993\}.$
(i) Prove that $S$ is an infinite set.
(ii) Find the least positive integer in $S.$
(iii) If all the elements of $S$ are written in ascending order as $$n_1 < n_2 < n_3 < \ldots ,$$ show that $$\lim_{i\rightarrow\infty} \frac{n_{i+1}}{n_i} = 3.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1993