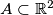
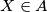
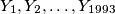
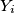
Show that there exists a finite set such that for every there are points in such that the distance between and is equal to 1, for every
%V0
Show that there exists a finite set $A \subset \mathbb{R}^2$ such that for every $X \in A$ there are points $Y_1, Y_2, \ldots, Y_{1993}$ in $A$ such that the distance between $X$ and $Y_i$ is equal to 1, for every $i.$
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
such that for every 
there are points 
in 
such that the distance between 
and 
is equal to 1, for every 