IMO Shortlist 1993 problem A5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0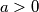 and
and  ,
,  are integers such that
are integers such that 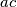 –
– 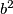 is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let
is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let  be the number of pairs of integers
be the number of pairs of integers 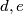 such that
such that 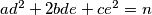 . Show that
. Show that is finite and that
is finite and that 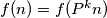 for every positive integer
for every positive integer  .
. Original Statement:
Let
 be given integers
be given integers 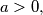
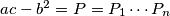 where
where 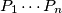 are (distinct) prime numbers. Let
are (distinct) prime numbers. Let 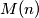 denote the number of pairs of integers
denote the number of pairs of integers  for which
for which 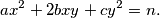 Prove that
Prove that 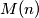 is finite and
is finite and 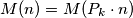 for every integer
for every integer 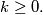 Note that the "
Note that the " " in
" in 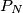 and the "
and the " " in
" in 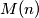 do not have to be the same.
do not have to be the same. Izvor: Međunarodna matematička olimpijada, shortlist 1993
 Školjka
Školjka 
