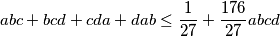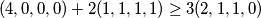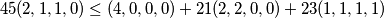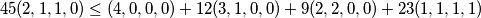grga, 18. travnja 2012. 15:07
kul, fora :)
pogledat cu kad nadem vremena
%V0
kul, fora :)
pogledat cu kad nadem vremena
Buco, 18. travnja 2012. 11:23
Mislim da ti ovo može pomoći s onime što si htio pokazati Grga :)
Općenito mislim da ste me bili pitali nekaj takvoga pa možda vam ovo posluži ako kakav takav odgovor.
Inače vux ovo je praktično trivijalno analizom rješiti ne shvaćam zašto inzistiraš na imenu Lagrangeovi multiplikatori kada se radi o običnoj derivaciji.
http://rijulsaini.wordpress.com/2010/10/28/schurs-inequality-for-four-variables/
%V0
Mislim da ti ovo može pomoći s onime što si htio pokazati Grga :)
Općenito mislim da ste me bili pitali nekaj takvoga pa možda vam ovo posluži ako kakav takav odgovor.
Inače vux ovo je praktično trivijalno analizom rješiti ne shvaćam zašto inzistiraš na imenu Lagrangeovi multiplikatori kada se radi o običnoj derivaciji.
http://rijulsaini.wordpress.com/2010/10/28/schurs-inequality-for-four-variables/
Zadnja promjena:
Buco, 18. travnja 2012. 11:23
vux, 17. travnja 2012. 20:58
ne ometaj me dok ga napadam lagrangeom :D
%V0
ne ometaj me dok ga napadam lagrangeom :D
grga, 17. travnja 2012. 20:30
xD
evo ako nekoga zanima rjesenje:
nije cak ni tesko za shvatit, al koristi malo ( bar meni ) ne tako poznatu metodu
http://awesomemath.org/wp-content/uploads/reflections/2006_6/2006_6_mixing.pdf
%V0
xD
evo ako nekoga zanima rjesenje:
nije cak ni tesko za shvatit, al koristi malo ( bar meni ) ne tako poznatu metodu
http://awesomemath.org/wp-content/uploads/reflections/2006_6/2006_6_mixing.pdf
vux, 17. travnja 2012. 20:11
ja bi ovaj zadatak napao lagrangeovim multiplikatorima...
%V0
ja bi ovaj zadatak napao lagrangeovim multiplikatorima...
grga, 17. travnja 2012. 20:05
jel bi znao itko pokazat
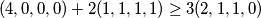
to vrijedi, al neznam dokazati, a iz toga slijedi zadatak.
hahaha :D drugi clan s desne strane mozes oslabiti na treci. odnosno, vrijedi i:
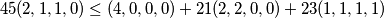
to je to sto se da oslabiti
%V0
jel bi znao itko pokazat
$(4,0,0,0) + 2(1,1,1,1) \geq 3(2,1,1,0)$
to vrijedi, al neznam dokazati, a iz toga slijedi zadatak.
[quote]hahaha :D drugi clan s desne strane mozes oslabiti na treci. odnosno, vrijedi i:
$45(2,1,1,0) \leq (4,0,0,0) + 21(2,2,0,0) + 23(1,1,1,1)$
to je to sto se da oslabiti[/quote]
Zadnja promjena:
grga, 17. travnja 2012. 20:05
grga, 15. travnja 2012. 18:44
cevid, ti si mi jednom spominjo one neke "vietine" nejednakosti..
jel mislis da bi mogao probat ovo rjesit pomocu toga?
%V0
cevid, ti si mi jednom spominjo one neke "vietine" nejednakosti..
jel mislis da bi mogao probat ovo rjesit pomocu toga?
ikicic, 15. travnja 2012. 18:27
hahaha :D drugi clan s desne strane mozes oslabiti na treci. odnosno, vrijedi i:
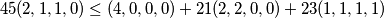
to je to sto se da oslabiti
%V0
hahaha :D drugi clan s desne strane mozes oslabiti na treci. odnosno, vrijedi i:
$45(2,1,1,0) \leq (4,0,0,0) + 21(2,2,0,0) + 23(1,1,1,1)$
to je to sto se da oslabiti
grga, 15. travnja 2012. 16:39
koga zanima, ovo je ekviv sa
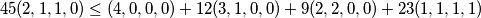
kico, aj probaj popravit koeficijente, bas me zanima dal se moze :P ( ja sam reinstaliro windowse u meduvremenu pa nemam vise program )
%V0
koga zanima, ovo je ekviv sa
$45 (2, 1, 1, 0) \leq (4, 0, 0, 0) + 12 (3, 1, 0, 0) + 9 (2, 2, 0, 0) + 23 (1, 1, 1, 1)$
kico, aj probaj popravit koeficijente, bas me zanima dal se moze :P ( ja sam reinstaliro windowse u meduvremenu pa nemam vise program )
grga, 15. travnja 2012. 16:17
ikicic, 14. travnja 2012. 22:37
hehe, dogadja se :) nismo jos te shortliste provjerali
%V0
hehe, dogadja se :) nismo jos te shortliste provjerali
vux, 14. travnja 2012. 21:16
Dakle koristeći nejednakost Gaastroma, dobijamo da vrijedi:
{{ INVALID LATEX }},
a sada koristeći uvjet dobijamo da vrijedi:
{{ INVALID LATEX }},
iz čega slijedi rješenje iz AG nejednakosti.
:D ajmo ekipa još par tih nedostataka sredit pa sve štima, nije lako bilo sve ovo ubacit sve te silne zadatke, svaka čast i samo naprijed :D
%V0
Dakle koristeći nejednakost Gaastroma, dobijamo da vrijedi:
{{ INVALID LATEX }},
a sada koristeći uvjet dobijamo da vrijedi:
{{ INVALID LATEX }},
iz čega slijedi rješenje iz AG nejednakosti.
:D ajmo ekipa još par tih nedostataka sredit pa sve štima, nije lako bilo sve ovo ubacit sve te silne zadatke, svaka čast i samo naprijed :D
Zadnja promjena:
vux, 14. travnja 2012. 21:17
Filip_Wee, 14. travnja 2012. 20:43
 Školjka
Školjka 

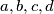 be four non-negative numbers satisfying
be four non-negative numbers satisfying 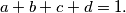 Prove the inequality
Prove the inequality