IMO Shortlist 1993 problem C1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 a) Show that the set 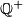 of all positive rationals can be partitioned into three disjoint subsets.
of all positive rationals can be partitioned into three disjoint subsets.  satisfying the following conditions:
satisfying the following conditions: 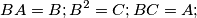 where
where 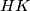 stands for the set
stands for the set 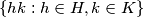 for any two subsets
for any two subsets 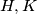 of
of 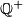 and
and 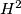 stands for
stands for 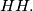
b) Show that all positive rational cubes are in for such a partition of
for such a partition of 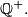
c) Find such a partition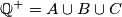 with the property that for no positive integer
with the property that for no positive integer 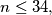 both
both  and
and  are in
are in  that is,
that is, 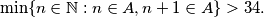
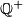 of all positive rationals can be partitioned into three disjoint subsets.
of all positive rationals can be partitioned into three disjoint subsets.  satisfying the following conditions:
satisfying the following conditions: 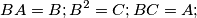 where
where 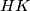 stands for the set
stands for the set 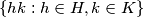 for any two subsets
for any two subsets 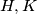 of
of 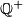 and
and 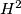 stands for
stands for 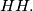
b) Show that all positive rational cubes are in
 for such a partition of
for such a partition of 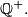
c) Find such a partition
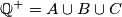 with the property that for no positive integer
with the property that for no positive integer 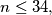 both
both  and
and  are in
are in  that is,
that is, 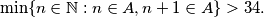
Izvor: Međunarodna matematička olimpijada, shortlist 1993
 Školjka
Školjka 
