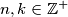
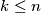
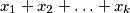
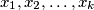
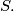
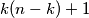
Let with and let be a set containing distinct real numbers. Let be a set of all real numbers of the form where are distinct elements of Prove that contains at least distinct elements.
%V0
Let $n,k \in \mathbb{Z}^{+}$ with $k \leq n$ and let $S$ be a set containing $n$ distinct real numbers. Let $T$ be a set of all real numbers of the form $x_1 + x_2 + \ldots + x_k$ where $x_1, x_2, \ldots, x_k$ are distinct elements of $S.$ Prove that $T$ contains at least $k(n-k)+1$ distinct elements.
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
with 
and let 
be a set containing 
distinct real numbers. Let 
be a set of all real numbers of the form 
where 
are distinct elements of 
Prove that 
distinct elements.