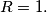
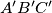
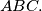
Let triangle be such that its circumradius is Let be the inradius of and let be the inradius of the orthic triangle of triangle Prove that
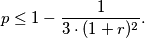
%V0
Let triangle $ABC$ be such that its circumradius is $R = 1.$ Let $r$ be the inradius of $ABC$ and let $p$ be the inradius of the orthic triangle $A'B'C'$ of triangle $ABC.$ Prove that $$p \leq 1 - \frac{1}{3 \cdot (1+r)^2}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
be such that its circumradius is 
Let 
be the inradius of 
be the inradius of the orthic triangle 
of triangle 
Prove that 