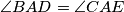
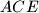
Given a triangle , let and be points on the side such that . If and are, respectively, the points of tangency of the incircles of the triangles and with the line , then show that
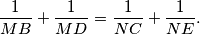
%V0
Given a triangle $ABC$, let $D$ and $E$ be points on the side $BC$ such that $\angle BAD = \angle CAE$. If $M$ and $N$ are, respectively, the points of tangency of the incircles of the triangles $ABD$ and $ACE$ with the line $BC$, then show that
$$\frac{1}{MB}+\frac{1}{MD}= \frac{1}{NC}+\frac{1}{NE}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
, let 
and 
be points on the side 
such that 
. If 
and 
are, respectively, the points of tangency of the incircles of the triangles 
and 
with the line 