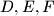
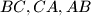
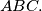
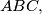
The vertices of an equilateral triangle lie on the sides respectively of a triangle If are the respective lengths of these sides, and the area of prove that
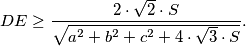
%V0
The vertices $D,E,F$ of an equilateral triangle lie on the sides $BC,CA,AB$ respectively of a triangle $ABC.$ If $a,b,c$ are the respective lengths of these sides, and $S$ the area of $ABC,$ prove that
$$DE \geq \frac{2 \cdot \sqrt{2} \cdot S}{\sqrt{a^2 + b^2 + c^2 + 4 \cdot \sqrt{3} \cdot S}}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
of an equilateral triangle lie on the sides 
respectively of a triangle 
If 
are the respective lengths of these sides, and 
the area of 
prove that 