IMO Shortlist 1993 problem N1
Dodao/la:
arhiva2. travnja 2012. A natural number

is said to have the property
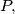
if, for all
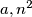
divides
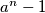
whenever

divides
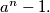
a.) Show that every prime number

has property
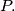
b.) Show that there are infinitely many composite numbers

that possess property
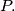
%V0
A natural number $n$ is said to have the property $P,$ if, for all $a, n^2$ divides $a^n - 1$ whenever $n$ divides $a^n - 1.$
a.) Show that every prime number $n$ has property $P.$
b.) Show that there are infinitely many composite numbers $n$ that possess property $P.$
Izvor: Međunarodna matematička olimpijada, shortlist 1993