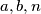
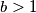
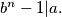
Let be positive integers, and Show that the representation of the number in the base contains at least digits different from zero.
%V0
Let $a,b,n$ be positive integers, $b > 1$ and $b^n-1|a.$ Show that the representation of the number $a$ in the base $b$ contains at least $n$ digits different from zero.
Izvor: Međunarodna matematička olimpijada, shortlist 1993
Školjka 
be positive integers, 
and 
Show that the representation of the number 
in the base 
contains at least 
digits different from zero.