IMO Shortlist 1994 problem A4
Dodao/la:
arhiva2. travnja 2012. Let
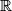
denote the set of all real numbers and
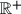
the subset of all positive ones. Let

and

be given elements in
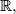
not necessarily distinct. Find all functions
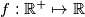
such that
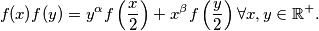
%V0
Let $\mathbb{R}$ denote the set of all real numbers and $\mathbb{R}^+$ the subset of all positive ones. Let $\alpha$ and $\beta$ be given elements in $\mathbb{R},$ not necessarily distinct. Find all functions $f: \mathbb{R}^+ \mapsto \mathbb{R}$ such that
$$f(x)f(y) = y^{\alpha} f \left( \frac{x}{2} \right) + x^{\beta} f \left( \frac{y}{2} \right) \forall x,y \in \mathbb{R}^+.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1994