IMO Shortlist 1994 problem A5
Dodao/la:
arhiva2. travnja 2012. Let
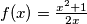
for
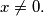
Define
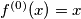
and
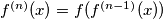
for all positive integers

and
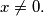
Prove that for all non-negative integers

and
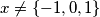
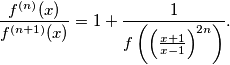
%V0
Let $f(x) = \frac{x^2+1}{2x}$ for $x \neq 0.$ Define $f^{(0)}(x) = x$ and $f^{(n)}(x) = f(f^{(n-1)}(x))$ for all positive integers $n$ and $x \neq 0.$ Prove that for all non-negative integers $n$ and $x \neq \{-1,0,1\}$
$$\frac{f^{(n)}(x)}{f^{(n+1)}(x)} = 1 + \frac{1}{f \left( \left( \frac{x+1}{x-1} \right)^{2n} \right)}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1994