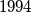
girls are seated at a round table. Initially one girl holds tokens. Each turn a girl who is holding more than one token passes one token to each of her neighbours.
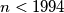
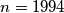
a.) Show that if , the game must terminate. b.) Show that if it cannot terminate.
%V0
$1994$ girls are seated at a round table. Initially one girl holds $n$ tokens. Each turn a girl who is holding more than one token passes one token to each of her neighbours.
a.) Show that if $n < 1994$, the game must terminate.
b.) Show that if $n = 1994$ it cannot terminate.
Izvor: Međunarodna matematička olimpijada, shortlist 1994
Školjka 
girls are seated at a round table. Initially one girl holds 
tokens. Each turn a girl who is holding more than one token passes one token to each of her neighbours. 
, the game must terminate. 
it cannot terminate.