IMO Shortlist 1994 problem G1
Dodao/la:
arhiva2. travnja 2012. 
and

are points on a semicircle. The tangent at

meets the extended diameter of the semicircle at

, and the tangent at

meets it at

, so that

and

are on opposite sides of the center. The lines

and

meet at

.

is the foot of the perpendicular from

to

. Show that

bisects angle
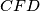
%V0
$C$ and $D$ are points on a semicircle. The tangent at $C$ meets the extended diameter of the semicircle at $B$, and the tangent at $D$ meets it at $A$, so that $A$ and $B$ are on opposite sides of the center. The lines $AC$ and $BD$ meet at $E$. $F$ is the foot of the perpendicular from $E$ to $AB$. Show that $EF$ bisects angle $CFD$
Izvor: Međunarodna matematička olimpijada, shortlist 1994