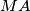
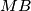
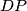
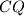
is a quadrilateral with parallel to . is the midpoint of , is the midpoint of and is the midpoint of . The lines and meet at . Prove that is inside the quadrilateral .
%V0
$ABCD$ is a quadrilateral with $BC$ parallel to $AD$. $M$ is the midpoint of $CD$, $P$ is the midpoint of $MA$ and $Q$ is the midpoint of $MB$. The lines $DP$ and $CQ$ meet at $N$. Prove that $N$ is inside the quadrilateral $ABCD$.
Izvor: Međunarodna matematička olimpijada, shortlist 1994
Školjka 
is a quadrilateral with 
parallel to 
. 
is the midpoint of 
, 
is the midpoint of 
and 
is the midpoint of 
. The lines 
and 
meet at 
. Prove that