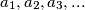
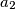
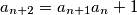
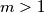
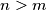
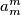
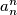
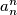
Define the sequence as follows. and are coprime positive integers and . Show that for every there is an such that divides . Is it true that must divide for some ?
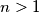
%V0
Define the sequence $a_1, a_2, a_3, ...$ as follows. $a_1$ and $a_2$ are coprime positive integers and $a_{n + 2} = a_{n + 1}a_n + 1$. Show that for every $m > 1$ there is an $n > m$ such that $a_m^m$ divides $a_n^n$. Is it true that $a_1$ must divide $a_n^n$ for some $n > 1$?
Izvor: Međunarodna matematička olimpijada, shortlist 1994
Školjka 
as follows. 
and 
are coprime positive integers and 
. Show that for every 
there is an 
such that 
divides 
. Is it true that 
?