IMO Shortlist 1995 problem A2
Dodao/la:
arhiva2. travnja 2012. Let

and

be non-negative integers such that
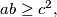
where

is an integer. Prove that there is a number

and integers
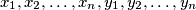
such that
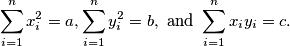
%V0
Let $a$ and $b$ be non-negative integers such that $ab \geq c^2,$ where $c$ is an integer. Prove that there is a number $n$ and integers $x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_n$ such that
$$\sum^n_{i=1} x^2_i = a, \sum^n_{i=1} y^2_i = b, \text{ and } \sum^n_{i=1} x_iy_i = c.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1995