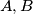
Let and be non-collinear points. Prove that there is a unique point in the plane of such that
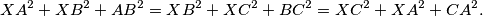
%V0
Let $A, B$ and $C$ be non-collinear points. Prove that there is a unique point $X$ in the plane of $ABC$ such that $$XA^2 + XB^2 + AB^2 = XB^2 + XC^2 + BC^2 = XC^2 + XA^2 + CA^2.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1995
Školjka 
and 
be non-collinear points. Prove that there is a unique point 
in the plane of 
such that 