IMO Shortlist 1995 problem G4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 An acute triangle  is given. Points
is given. Points  and
and  are taken on the side
are taken on the side  (with
(with  between
between  and
and  ),
),  and
and  on the side
on the side  (with
(with  between
between  and
and  ), and
), and  and
and 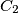 on the side
on the side  (with
(with 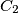 between
between  and
and  ) so that
) so that
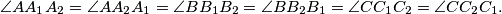
The lines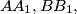 and
and 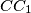 bound a triangle, and the lines
bound a triangle, and the lines 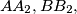 and
and 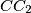 bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
 is given. Points
is given. Points  and
and  are taken on the side
are taken on the side  (with
(with  between
between  and
and  ),
),  and
and  on the side
on the side  (with
(with  between
between  and
and  ), and
), and  and
and 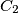 on the side
on the side  (with
(with 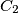 between
between  and
and  ) so that
) so that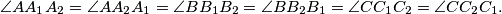
The lines
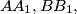 and
and 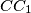 bound a triangle, and the lines
bound a triangle, and the lines 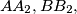 and
and 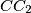 bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle. Izvor: Međunarodna matematička olimpijada, shortlist 1995
 Školjka
Školjka 
