IMO Shortlist 1995 problem G7
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 Let ABCD be a convex quadrilateral and O a point inside it. Let the parallels to the lines BC, AB, DA, CD through the point O meet the sides AB, BC, CD, DA of the quadrilateral ABCD at the points E, F, G, H, respectively. Then, prove that 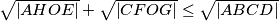 , where
, where 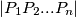 is an abbreviation for the non-directed area of an arbitrary polygon
is an abbreviation for the non-directed area of an arbitrary polygon 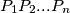 .
.
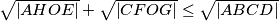 , where
, where 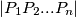 is an abbreviation for the non-directed area of an arbitrary polygon
is an abbreviation for the non-directed area of an arbitrary polygon 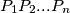 .
. Izvor: Međunarodna matematička olimpijada, shortlist 1995
 Školjka
Školjka 
