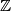
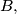
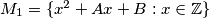
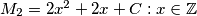
Let denote the set of all integers. Prove that for any integers and one can find an integer for which and do not intersect.
%V0
Let $\mathbb{Z}$ denote the set of all integers. Prove that for any integers $A$ and $B,$ one can find an integer $C$ for which $M_1 = \{x^2 + Ax + B : x \in \mathbb{Z}\}$ and $M_2 = {2x^2 + 2x + C : x \in \mathbb{Z}}$ do not intersect.
Izvor: Međunarodna matematička olimpijada, shortlist 1995
Školjka 
denote the set of all integers. Prove that for any integers 
and 
one can find an integer 
for which 
and 
do not intersect.