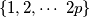
Let be an odd prime number. How many -element subsets of are there, the sum of whose elements is divisible by ?
%V0
Let $p$ be an odd prime number. How many $p$-element subsets $A$ of $\{1,2,\cdots \ 2p\}$ are there, the sum of whose elements is divisible by $p$?
Izvor: Međunarodna matematička olimpijada, shortlist 1995
Školjka 
be an odd prime number. How many 
of 
are there, the sum of whose elements is divisible by