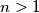
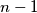
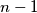
Does there exist an integer which satisfies the following condition? The set of positive integers can be partitioned into nonempty subsets, such that an arbitrary sum of integers, one taken from each of any of the subsets, lies in the remaining subset.
%V0
Does there exist an integer $n > 1$ which satisfies the following condition? The set of positive integers can be partitioned into $n$ nonempty subsets, such that an arbitrary sum of $n - 1$ integers, one taken from each of any $n - 1$ of the subsets, lies in the remaining subset.
Izvor: Međunarodna matematička olimpijada, shortlist 1995
Školjka 
which satisfies the following condition? The set of positive integers can be partitioned into 
nonempty subsets, such that an arbitrary sum of 
integers, one taken from each of any