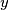
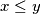
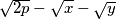
Let be an odd prime. Determine positive integers and for which and is non-negative and as small as possible.
%V0
Let $p$ be an odd prime. Determine positive integers $x$ and $y$ for which $x \leq y$ and $\sqrt{2p} - \sqrt{x} - \sqrt{y}$ is non-negative and as small as possible.
Izvor: Međunarodna matematička olimpijada, shortlist 1995
Školjka 
be an odd prime. Determine positive integers 
and 
for which 
and 
is non-negative and as small as possible.