IMO Shortlist 1995 problem S1
Dodao/la:
arhiva2. travnja 2012. Does there exist a sequence
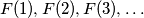
of non-negative integers that simultaneously satisfies the following three conditions?
(a) Each of the integers
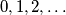
occurs in the sequence.
(b) Each positive integer occurs in the sequence infinitely often.
(c) For any
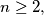
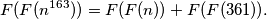
%V0
Does there exist a sequence $F(1), F(2), F(3), \ldots$ of non-negative integers that simultaneously satisfies the following three conditions?
(a) Each of the integers $0, 1, 2, \ldots$ occurs in the sequence.
(b) Each positive integer occurs in the sequence infinitely often.
(c) For any $n \geq 2,$
$$F(F(n^{163})) = F(F(n)) + F(F(361)).$$
Izvor: Međunarodna matematička olimpijada, shortlist 1995