IMO Shortlist 1995 problem S3
Dodao/la:
arhiva2. travnja 2012. For an integer
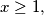
let
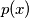
be the least prime that does not divide
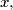
and define
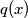
to be the product of all primes less than
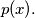
In particular,
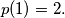
For

having
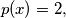
define
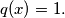
Consider the sequence
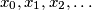
defined by
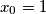
and
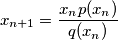
for
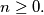
Find all

such that
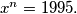
%V0
For an integer $x \geq 1,$ let $p(x)$ be the least prime that does not divide $x,$ and define $q(x)$ to be the product of all primes less than $p(x).$ In particular, $p(1) = 2.$ For $x$ having $p(x) = 2,$ define $q(x) = 1.$ Consider the sequence $x_0, x_1, x_2, \ldots$ defined by $x_0 = 1$ and
$$x_{n+1} = \frac{x_n p(x_n)}{q(x_n)}$$ for $n \geq 0.$ Find all $n$ such that $x^n = 1995.$
Izvor: Međunarodna matematička olimpijada, shortlist 1995