IMO Shortlist 1995 problem S4
Dodao/la:
arhiva2. travnja 2012. Suppose that
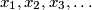
are positive real numbers for which
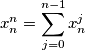
for
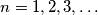
Prove that
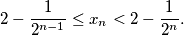
%V0
Suppose that $x_1, x_2, x_3, \ldots$ are positive real numbers for which $$x^n_n = \sum^{n-1}_{j=0} x^j_n$$ for $n = 1, 2, 3, \ldots$ Prove that $\forall n,$ $$2 - \frac{1}{2^{n-1}} \leq x_n < 2 - \frac{1}{2^n}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1995