IMO Shortlist 1995 problem S5
Dodao/la:
arhiva2. travnja 2012. For positive integers
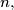
the numbers

are defined inductively as follows:
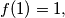
and for every positive integer
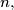
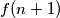
is the greatest integer

such that there is an arithmetic progression of positive integers
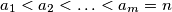
for which
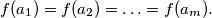
Prove that there are positive integers

and

such that
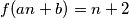
for every positive integer

%V0
For positive integers $n,$ the numbers $f(n)$ are defined inductively as follows: $f(1) = 1,$ and for every positive integer $n,$ $f(n+1)$ is the greatest integer $m$ such that there is an arithmetic progression of positive integers $a_1 < a_2 < \ldots < a_m = n$ for which
$$f(a_1) = f(a_2) = \ldots = f(a_m).$$
Prove that there are positive integers $a$ and $b$ such that $f(an+b) = n+2$ for every positive integer $n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1995