IMO Shortlist 1996 problem A3
Dodao/la:
arhiva2. travnja 2012. Let
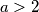
be given, and starting
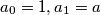
define recursively:
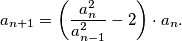
Show that for all integers
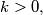
we have:
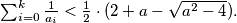
%V0
Let $a > 2$ be given, and starting $a_0 = 1, a_1 = a$ define recursively:
$$a_{n+1} = \left(\frac{a^2_n}{a^2_{n-1}} - 2 \right) \cdot a_n.$$
Show that for all integers $k > 0,$ we have: $\sum^k_{i = 0} \frac{1}{a_i} < \frac12 \cdot (2 + a - \sqrt{a^2-4}).$
Izvor: Međunarodna matematička olimpijada, shortlist 1996