IMO Shortlist 1996 problem A4
Dodao/la:
arhiva2. travnja 2012. Let
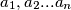
be non-negative reals, not all zero. Show that that
(a) The polynomial
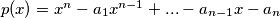
has preceisely 1 positive real root

.
(b) let
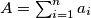
and
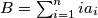
. Show that
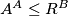
.
%V0
Let $a_{1}, a_{2}...a_{n}$ be non-negative reals, not all zero. Show that that
(a) The polynomial $p(x) = x^{n} - a_{1}x^{n - 1} + ... - a_{n - 1}x - a_{n}$ has preceisely 1 positive real root $R$.
(b) let $A = \sum_{i = 1}^n a_{i}$ and $B = \sum_{i = 1}^n ia_{i}$. Show that $A^{A} \leq R^{B}$.
Izvor: Međunarodna matematička olimpijada, shortlist 1996