IMO Shortlist 1996 problem A9
Dodao/la:
arhiva2. travnja 2012. Let the sequence
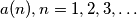
be generated as follows with
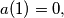
and for


1.) Determine the maximum and minimum value of
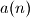
over
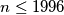
and find all
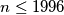
for which these extreme values are attained.
2.) How many terms
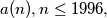
are equal to 0?
%V0
Let the sequence $a(n), n = 1,2,3, \ldots$ be generated as follows with $a(1) = 0,$ and for $n > 1:$
$$a(n) = a\left( \left \lfloor \frac{n}{2} \right \rfloor \right) + (-1)^{\frac{n(n+1)}{2}}.$$
1.) Determine the maximum and minimum value of $a(n)$ over $n \leq 1996$ and find all $n \leq 1996$ for which these extreme values are attained.
2.) How many terms $a(n), n \leq 1996,$ are equal to 0?
Izvor: Međunarodna matematička olimpijada, shortlist 1996