IMO Shortlist 1996 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Determine whether or nor there exist two disjoint infinite sets  and
and  of points in the plane satisfying the following conditions:
of points in the plane satisfying the following conditions:
a.) No three points in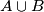 are collinear, and the distance between any two points in
are collinear, and the distance between any two points in 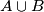 is at least 1.
is at least 1.
b.) There is a point of in any triangle whose vertices are in
in any triangle whose vertices are in 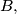 and there is a point of
and there is a point of  in any triangle whose vertices are in
in any triangle whose vertices are in 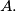
 and
and  of points in the plane satisfying the following conditions:
of points in the plane satisfying the following conditions: a.) No three points in
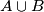 are collinear, and the distance between any two points in
are collinear, and the distance between any two points in 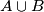 is at least 1.
is at least 1. b.) There is a point of
 in any triangle whose vertices are in
in any triangle whose vertices are in 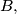 and there is a point of
and there is a point of  in any triangle whose vertices are in
in any triangle whose vertices are in 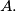
Izvor: Međunarodna matematička olimpijada, shortlist 1996
 Školjka
Školjka 
