IMO Shortlist 1996 problem G4
Dodao/la:
arhiva2. travnja 2012. Let

be an equilateral triangle and let

be a point in its interior. Let the lines
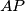
,
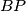
,
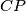
meet the sides

,

,

at the points

,

,

, respectively. Prove that
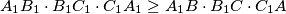
.
%V0
Let $ABC$ be an equilateral triangle and let $P$ be a point in its interior. Let the lines $AP$, $BP$, $CP$ meet the sides $BC$, $CA$, $AB$ at the points $A_1$, $B_1$, $C_1$, respectively. Prove that
$A_1B_1 \cdot B_1C_1 \cdot C_1A_1 \ge A_1B \cdot B_1C \cdot C_1A$.
Izvor: Međunarodna matematička olimpijada, shortlist 1996