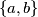
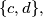
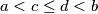
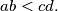
Let the sides of two rectangles be and respectively, with and Prove that the first rectangle can be placed within the second one if and only if
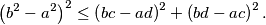
%V0
Let the sides of two rectangles be $\{a,b\}$ and $\{c,d\},$ respectively, with $a < c \leq d < b$ and $ab < cd.$ Prove that the first rectangle can be placed within the second one if and only if
$$\left(b^2 - a^2\right)^2 \leq \left(bc - ad \right)^2 + \left(bd - ac \right)^2.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1996
Školjka 
and 
respectively, with 
and 
Prove that the first rectangle can be placed within the second one if and only if 