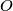
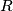
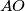
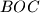
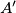
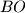
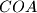
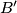
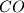
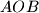
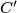
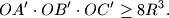
Let be an acute triangle with circumcenter and circumradius . meets the circumcircle of at , meets the circumcircle of at and meets the circumcircle of at . Prove that Sorry if this has been posted before since this is a very classical problem, but I failed to find it with the search-function.
%V0
Let $ABC$ be an acute triangle with circumcenter $O$ and circumradius $R$. $AO$ meets the circumcircle of $BOC$ at $A'$, $BO$ meets the circumcircle of $COA$ at $B'$ and $CO$ meets the circumcircle of $AOB$ at $C'$. Prove that $$OA'\cdot OB'\cdot OC'\geq 8R^{3}.$$ Sorry if this has been posted before since this is a very classical problem, but I failed to find it with the search-function.
Izvor: Međunarodna matematička olimpijada, shortlist 1996
Školjka 
be an acute triangle with circumcenter 
and circumradius 
. 
meets the circumcircle of 
at 
, 
meets the circumcircle of 
at 
and 
meets the circumcircle of 
at 
. Prove that 
Sorry if this has been posted before since this is a very classical problem, but I failed to find it with the search-function.