IMO Shortlist 1996 problem G9
Dodao/la:
arhiva2. travnja 2012. In the plane, consider a point

and a polygon
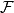
(which is not necessarily convex). Let

denote the perimeter of
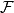
, let

be the sum of the distances from the point

to the vertices of
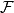
, and let

be the sum of the distances from the point

to the sidelines of
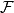
. Prove that
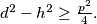
%V0
In the plane, consider a point $X$ and a polygon $\mathcal{F}$ (which is not necessarily convex). Let $p$ denote the perimeter of $\mathcal{F}$, let $d$ be the sum of the distances from the point $X$ to the vertices of $\mathcal{F}$, and let $h$ be the sum of the distances from the point $X$ to the sidelines of $\mathcal{F}$. Prove that $d^2 - h^2\geq\frac {p^2}{4}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1996